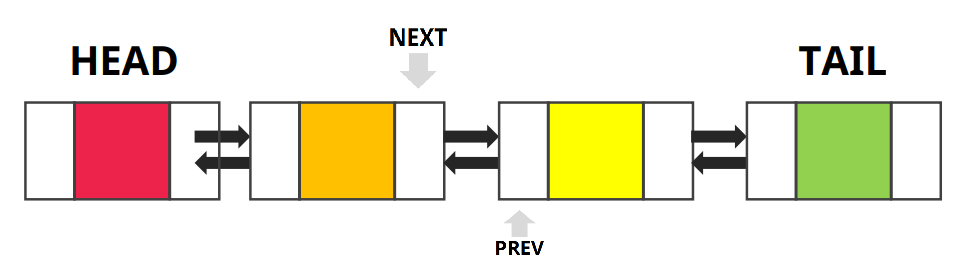
1. Double Linked List 개념
Pointer가 앞뒤로 두 개가 들어가기 때문에 동일 데이터 양의 Single Linked List 보다 더 많은 용량이 필요하다.
데이터 추가 시 Tail Node로 접근해서 데이터 추가가 가능하다.
데이터 검색/삽입 시 인덱스가 Head보다 Tail에 가까우면 Tail로 타고 들어가서 검색/삽입이 가능하다.
따라서 Double Linked List는 더 많은 필요 용량에도 불구하고 성능 상 나름의 장점을 가지게 된다.
(시간 복잡도로는 Single Linked List와 동일하게 O(n)이지만 연산 속도가 더 짧을 것으로 예상할 수 있다)
2. Double Linked List 구현 (JAVA)
single Linked List와 마찬가지로 Node 기반으로 구현을 하기 때문에
가장 먼저 Private Class Node를 먼저 생성해 준다.
Head와 Tail Node는 더미 노드로 데이터가 없는 채로 구현한다.
package list;
public class MyDoubleLinkedList<T> implements IList<T> {
private Node head; // Head, Tail Node 각각 생성, 데이터 사이즈 변수 생성
private Node tail;
private int size;
public MyDoubleLinkedList() { // 초기화를 위한 생성자
this.size = 0;
this.head = new Node(null);
this.tail = new Node(null);
this.head.next = this.tail;
this.tail.prev = this.head;
// size()
// clear()
// add()
}
@Override
public void add(T t) { // Tail 바로 앞에 데이터(t)를 삽입하는 동작
Node last = this.tail.prev; // 맨끝 노드는 tail의 prev 노드이다
Node newNode = new Node(t, last, tail); // 새로만든 노드는 t 데이터를 가지고 prev로는 last를 next로는 tail를 가지게 된다.
last.next = newNode; // 기존 last는 next로 새로운 노드를 가지고
this.tail.prev = newNode; // tail은 prev로 새로운 노드를 가진다.
this.size++; // 데이터 사이즈 +1
// 그 다음 get(index)
}
@Override
public void insert(int index, T t) { // index를 통해 데이터를 삽입하는 동작
if (index > this.size || index < 0) {
throw new IndexOutOfBoundsException();
}
Node prev = null; // 반복문 돌릴 node 및 변수 초기화
Node current = null;
int i = 0;
if (index < this.size / 2) { // head에서 가까운 경우
prev = this.head;
current = this.head.next; // current가 index 0인 상황
while (i++ < index) { // current를 찾는 index까지 탐색해 들어옴
prev = prev.next;
current = current.next;
}
} else { // tail에서 가까운 경우
current = this.tail; // prev가 마지막 index 인 상황
prev = this.tail.prev;
while (i++ < (this.size - index)) {
current = current.prev;
prev = prev.prev;
}
}
Node newNode = new Node(t, prev, current); // 새로운 노드를 생성하고 포인터 연결
current.prev = newNode; // current 노드의 prev 포인터를 새로운 노드로 연결
prev.next = newNode; // prev 노드의 next 포인터를 새로운 노드로 연결
this.size++;
// 그 다음 delete by index
}
@Override
public void clear() { // 초기화로 돌리는 동작
this.size = 0;
this.head.next = this.tail;
this.head.prev = null;
this.tail.next = null;
this.tail.prev = this.head;
}
@Override
public boolean delete(T t) {
Node prev = this.head;
Node current = prev.next;
while (current != null) {
if (current.data.equals(t)) {
prev.next = current.next;
current.next.prev = prev;
current.next = null;
current.prev = null;
this.size--;
return true;
}
prev = prev.next;
current = current.next;
}
return false;
}
@Override
public boolean deleteByIndex(int index) { // 인덱스로 접근해 노드를 삭제하는 동작
if (index >= this.size || index < 0) {
throw new IndexOutOfBoundsException();
}
Node prev = null;
Node current = null;
Node next = null;
int i = 0;
if (index < this.size / 2) {
prev = this.head;
current = this.head.next;
while (i++ < index) {
prev = prev.next;
current = current.next;
}
prev.next = current.next;
current.next.prev = prev;
current.next = null;
current.prev = null;
} else {
current = this.tail.prev;
next = this.tail;
while (i++ < (this.size - index - 1)) {
next = next.prev;
current = current.prev;
}
next.prev = current.prev;
current.prev.next = next;
current.next = null;
current.prev = null;
}
this.size--;
return true;
}
@Override
public T get(int index) { // index로 데이터를 검색하는 동작
if (index >= this.size || index < 0) {
throw new IndexOutOfBoundsException();
}
int i = 0; // 반복문 돌릴 변수/노드 초기화
Node current = null;
if (index < this.size / 2) { // index가 Head에서 더 가까우면
current = this.head.next; // 첫번째 index
while (i++ < index) { // 앞에서 부터 index까지 node를 찾아들어가는 동작
current = current.next;
}
} else { // index가 Tail에서 더 가까우면
current = this.tail.prev; // 마지막 index
while (i++ < (this.size - index - 1)) { // 뒤에서 부터 index까지 node를 찾아들어가는 동작
current = current.prev;
}
}
return current.data;
// 그 다음 insert(index)
}
@Override
public int indexOf(T t) {
Node current = this.head.next;
int index = 0;
while (current != null) {
if (current.data != null && current.data.equals(t)) {
return index;
}
current = current.next;
index++;
}
return -1;
}
@Override
public boolean isEmpty() {
return this.head.next == this.tail;
}
@Override
public boolean contains(T t) {
Node current = this.head.next;
while (current != null) {
if (current.data != null && current.data.equals(t)) {
return true;
}
current = current.next;
}
return false;
}
@Override
public int size() { // 데이터 크기 반환 동작
return this.size;
}
private class Node { // Node class를 먼저 생성
T data;
Node prev;
Node next;
Node(T data) { // Node data 초기화 생성자
this.data = data;
}
Node(T data, Node prev, Node next) { // Node data 및 prev, next node 초기화 생성자
this.data = data;
this.prev = prev;
this.next = next;
}
}
}3. Double Linked List 구현 (Python)
class Node:
def __init__(self, data, prev_=None, next_=None):
self.data = data
self.prev = prev_
self.next = next_
class DoubleLinkedList:
def __init__(self):
self.head = Node(None)
self.tail = Node(None)
self._size = 0
self.head.next = self.tail
self.tail.prev = self.head
def size(self):
return self._size
def add(self, data):
last = self.tail.prev
new_node = Node(data, last, self.tail)
last.next = new_node
self.tail.prev = new_node
self._size += 1
def insert(self, index, data):
if index > self._size or index < 0:
raise RuntimeError("Index out of error")
prev, current = None, None
i = 0
if index < self._size // 2:
prev = self.head
current = self.head.next
while i < index:
prev = prev.next
current = current.next
i += 1
else:
current = self.tail
prev = self.tail.prev
while i < (self._size - index):
current = current.prev
prev = prev.prev
i += 1
new_node = Node(data, prev, current)
current.prev = new_node
prev.next = new_node
self._size += 1
def clear(self):
self._size = 0
self.head.next = self.tail
self.head.prev = None
self.tail.next = None
self.tail.prev = self.head
def delete(self, data):
prev = self.head
current = prev.next
while current is not None:
if current.data == data:
prev.next = current.next
current.next.prev = prev
current.next = None
current.prev = None
self._size -= 1
return True
prev = prev.next
current = current.next
return False
def delete_by_index(self, index):
if index >= self._size or index < 0:
raise RuntimeError("Index out of error")
prev_, current_, next_ = None, None, None
i = 0
if index < self._size // 2:
prev_ = self.head
current_ = self.head.next
while i < index:
prev_ = prev_.next
current_ = current_.next
i += 1
prev_.next = current_.next
current_.next.prev = prev_
current_.next = None
current_.prev = None
else:
current_ = self.tail.prev
next_ = self.tail
while i < (self._size - index - 1):
next_ = next_.prev
current_ = current_.prev
next_.prev = current_.rpev
current_.prev.next = next_
current_.next = None
current_.prev = None
self._size -= 1
return True
def get(self, index):
if index >= self._size or index < 0:
raise RuntimeError("Index out of error")
i = 0
current = None
if index < self.size // 2:
current = self.head.next
while i < index:
current = current.next
i += 1
else:
current = self.head.prev
while i < (self._size - index - 1):
current = current.prev
i += 1
return current.data
def index_of(self, data):
current = self.head.next
index = 0
while current != None:
if current.data != None and current.data == data:
return index
current = current.next
index += 1
return -1
def is_empty(self):
return self.head.next == self.tail
def contains(self, data):
current = self.head.next
while current != None:
if current.data != None and current.data == data:
return True
current = current.next
return False
if __name__ == "__main__":
l = DoubleLinkedList()
for elem in [3, 2, 5, 1, 4]:
print(f"l.add({elem})")
l.add(elem)
print(f"l.size(): {l.size()}")
print("=====================")
for elem in [3, 2, 5, 1, 4, 100]:
print(f"l.contains({elem}): {l.contains(elem)}")
print(f"l.index_of({elem}): {l.index_of(elem)}")
print("=====================")
for elem in [4, 5, 100]:
print(f"l.delete({elem}): {l.delete(elem)}")
print(f"l.size(): {l.size()}")
print(f"l.insert(0, 100)")
l.insert(0, 100)
print(f"l.insert(2, 101)")
l.insert(2, 101)
for elem in [3, 2, 5, 1, 4, 100, 101]:
print(f"l.contains({elem}): {l.contains(elem)}")
print(f"l.index_of({elem}): {l.index_of(elem)}")'Basic Computer Science > Data Structure' 카테고리의 다른 글
| 6. 스택(Stack) (0) | 2023.07.14 |
|---|---|
| 5. 리스트 - 알고리즘 문제 (0) | 2023.07.12 |
| 3. 리스트 - 연결리스트(Linked List) (0) | 2023.07.11 |
| 2. 리스트 -배열(Array List) (1) | 2023.07.10 |
| 1. 자료구조 기초 (0) | 2023.06.29 |
댓글