1. Merge Sort 개념
하나의 리스트를 두 개의 균등한 크기의 리스트로 분할하고(서브리스트의 크기가 1이 될때까지),
부분 리스트를 합치면서 정렬하여 전체가 정렬되도록 함.
분할 정복 (Divide and Conquer) 알고리즘 - 재귀함수 사용
분할
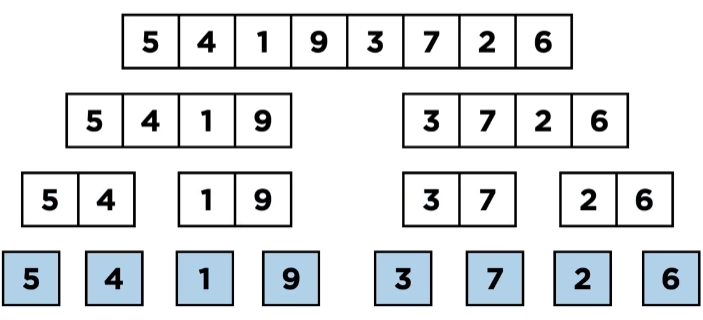
합병

시간복잡도 O(NlogN)
2. Merge Sort 구현 - JAVA
In-place 방식 구현
package sort;
public class MergeSort implements ISort {
// 안정 정렬
@Override
public void sort(int[] arr) {
mergeSort(arr, 0, arr.length - 1);
} //mergesort 배열 초기화
// 분할
private void mergeSort(int[] arr, int low, int high) {
if (low >= high) { // low 와 high 의 인덱스가 동일하다는 것 -> 배열의 크기가 1이 되는 경우
return;
}
// 실제로 arr 을 쪼개서 수많은 배열로 따로 만드는 게 아니라
// arr 가 둘씩 분할되는 인덱스 위치를 찾음
int mid = low + ((high - low) / 2); // 리스트의 중간 위치 인덱스. 중간 인덱스를 기준으로 분할
mergeSort(arr, low, mid); // 중간 인덱스를 기준으로 왼쪽 부분
mergeSort(arr, mid + 1, high); // 중간 인덱스를 기준으로 오른쪽 부분 재귀호출
// low, mid, high 에는 분할된 인덱스의 값이 있음
merge(arr, low, mid, high); // merge 하면서 정렬
}
private void merge(int arr[], int low, int mid, int high) {
int[] temp = new int[high - low + 1]; // 보조 배열
int idx = 0; // 보조 배열의 인덱스
int left = low; // 분할된 왼쪽 리스트의 시작 인덱스
int right = mid + 1; // 분할된 오른쪽 리스트의 시작 인덱스
while (left <= mid && right <= high) {
// left 나 right 인덱스 둘중 하나라도
// 리스트에 있는 값을 모두 꺼내게 되면 while 문이 종료
if (arr[left] <= arr[right]) { // 오름 차순 정렬해서 데이터를 쌓아야 하므로 작은 값부터
temp[idx] = arr[left];
left++;
} else {
temp[idx] = arr[right];
right++;
}
idx++;
}
while (left <= mid) { // 왼쪽 리스트에 아직 값이 남아 있는 경우
temp[idx] = arr[left];
idx++;
left++;
}
while (right <= high) { // 오른쪽 리스트에 아직 값이 남아 있는 경우
temp[idx] = arr[right];
idx++;
right++;
}
// 보조배열에 있는 값을 arr 로 복사
for (int i = low; i <= high; i++) {
arr[i] = temp[i - low];
}
}
}
수업으로만 잘 이해가 안되서 찾아본 영상
3. Merge Sort 구현 - Python
def merge_sort(arr):
if len(arr) <= 1:
return
# divide
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
merge_sort(left)
merge_sort(right)
# conquer
i = 0 # left idx
j = 0 # right idx
k = 0 # arr idx
while i < len(left) and j < len(right):
if left[i] <= right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1
while i < len(left):
arr[k] = left[i]
i += 1
k += 1
while j < len(right):
arr[k] = right[j]
j += 1
k += 1
if __name__ == "__main__":
arr = [9,1,6,3,7,2,8,4,5,0]
merge_sort(arr)
print(arr)'Basic Computer Science > Data Structure' 카테고리의 다른 글
| 17. 정렬(Sort) - 퀵 정렬(Quick Sort) (0) | 2023.09.02 |
|---|---|
| 15. 정렬(Sort) - 삽입정렬(Insert Sort) (0) | 2023.08.23 |
| 14. 정렬(Sort) - 버블정렬(Bubble Sort) (0) | 2023.08.23 |
| 13. 정렬(Sort) - 이진탐색(Binary Search) (0) | 2023.08.03 |
| 12. 해시 - 알고리즘 문제 (0) | 2023.08.02 |
댓글