1. Quick Sort 개념
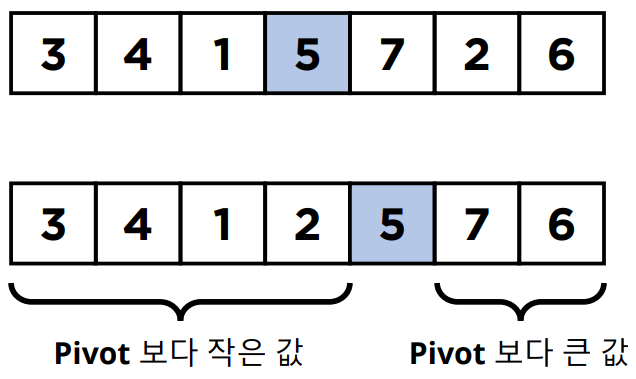
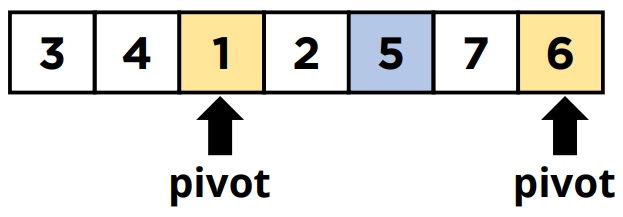
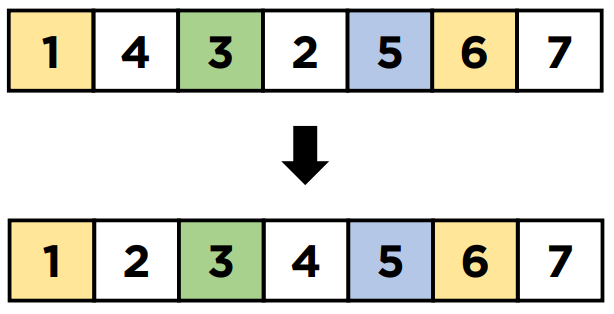
리스트에서 Pivot 값을 정하고 Pivot을 기준으로 나머지 값들의 크기를 비교하여 왼쪽과 오른쪽을 나눈다.
나눠진 리스트에서 다시 Pivot을 정하고 반복하여 정렬한다.
분할 정복 (Divide and Conquer) 알고리즘 - 재귀함수 사용
시간 복잡도 O(NlogN)으로 Merge Sort와 같으나 Locality of reference에 의해
실제로는 더 빠르다. (메인 메모리에 접근하지 않고 캐쉬에서 데이터를 불러오도록 유도한다)
최악의 시나리오 일 때 시간복잡도는 O(N2)으로 정렬된 리스트에서 가장 양끝에서 Pivot값이 정해질 때이다.
추가적인 메모리 공간을 사용하지 않는다.
불안정 정렬

Pivot값은 규칙을 정하기 나름인데 인덱스 가운데 값으로 설정하여 구현한 모습이다.


2. Quick Sort 구현 - JAVA
package sort;
public class QuickSort implements ISort {
@Override
public void sort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
} // quicksort내에 정렬하고자하는 배열 가장낮은 인덱스, 가장 높은 인덱스 입력
private void quickSort(int[] arr, int low, int high) {
// 분할된 배열의 크기가 1이 될 때까지
if (low >= high) {
return;
}
// pivot 인덱스
int pivot = low + ((high - low) / 2);
// pivot 인덱스에 위치한 값
int pivotValue = arr[pivot];
int left = low;
int right = high;
// 피봇값을 기준으로 피봇값의 왼쪽에는 피봇값보다 작은 값
// 오른쪽엔 피봇값보다 큰 값
while (left <= right) {
// 왼쪽 값이 피봇값보다 작으면
// 위치를 바꿀 필요가 없기 때문에 그대로 두고 왼쪽 인덱스를 증가
while (arr[left] < pivotValue) {
left++;
}
// 오른쪽 값이 피봇값보다 크면
// 위치를 바꿀 필요가 없기 때문에 계속 오른쪽 인덱스를 감소
while (arr[right] > pivotValue) {
right--;
}
// 왼쪽 인덱스와 오른쪽 인덱스가 교차 하지 않았으면 왼쪽 값과 오른쪽 값 교환
if (left <= right) {
int tmp = arr[right];
arr[right] = arr[left];
arr[left] = tmp;
left++;
right--;
}
}
quickSort(arr, low, right);
quickSort(arr, left, high);
}
}3. Quick Sort 구현 - Python
def quick_sort(arr):
__sort(arr, 0, len(arr) - 1)
def __sort(arr, low, high):
if low >= high:
return
pivot = (low + high) // 2
pivot_val = arr[pivot]
left, right = low, high
while left <= right:
while arr[left] < pivot_val:
left += 1
while arr[right] > pivot_val:
right -= 1
if left <= right:
arr[right], arr[left] = arr[left], arr[right]
left += 1
right -= 1
__sort(arr, low, right)
__sort(arr, left, high)
if __name__ == "__main__":
arr = [9,1,6,3,7,2,8,4,5,0]
quick_sort(arr)
print(arr)
'Basic Computer Science > Data Structure' 카테고리의 다른 글
| 16. 정렬(Sort) - 합병정렬(Merge Sort) (0) | 2023.08.24 |
|---|---|
| 15. 정렬(Sort) - 삽입정렬(Insert Sort) (0) | 2023.08.23 |
| 14. 정렬(Sort) - 버블정렬(Bubble Sort) (0) | 2023.08.23 |
| 13. 정렬(Sort) - 이진탐색(Binary Search) (0) | 2023.08.03 |
| 12. 해시 - 알고리즘 문제 (0) | 2023.08.02 |
댓글